Algoritmo detector de pulsos

Con este tutorial vamos a concluir la serie sobre análisis de audio utilizando la librería FMOD y Unreal Engine 4. En esta ocasión vamos a explicar como realizar un detector de pulso o ritmo en tiempo real. Este algoritmo no es una solución universal para todas las canciones pero es una aproximación aceptable teniendo en cuenta las limitaciones de tiempo de procesamiento.

Parte 1: Configurando las rutas del proyecto
Parte 2: Usando la librería
Parte 3: Espectro de Frecuencias
Parte 4: Visualizador de espectro para UE4
Parte 5: Algoritmo detector de pulsos
Parte 6: Visualizador de pulso para UE4

Hay muchos métodos disponibles y la detección del comienzo de un pulso es siempre una lucha entre exactitud y velocidad. Uno de los documentos que explican uno de estos métodos es Beat Detection Algorithms de Frédéric Patin. La idea básica del algoritmo es utilizar un modelo estadístico basado en la amplitud o energía del sonido. Podemos calcular la media de esa energía en un intervalo de tiempo de un par de segundos y compararla con la energía actual del sonido, si la diferencia de ambas sobrepasa un umbral determinado podemos considerar que se ha producido un pulso.

Utilizando un tamaño de ventana de 1024 muestras y una velocidad de muestreo de 44100Hz, necesitaremos un buffer de 44100/1024 = 43 elementos para guardar 1 segundo de historia. Los valores de estas muestras pueden obtenerse del análisis FFT, una explicación sobre como utilizar la FFT y FMOD puede encontrarse en un tutorial anterior Espectro de Frecuencias utilizando FMOD y UE4.

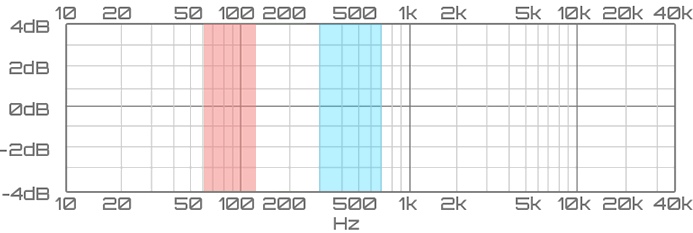
Vamos a centrar el análisis de pulso en las primeras barras del espectro, la razón de esto es que vamos a comprobar las frecuencias más bajas para capturar el uso del bombo y de la caja de una batería, uno de los instrumentos utilizados con más frecuencia para llevar el ritmo de la canciones. Para nuestro experimento vamos a establecer un rango entre 60hz-130hz para nuestra banda de Graves, en el que encontraremos el sonido de un bombo, y un rango Medios-Graves 301hz-750hz, en el que estará la mayoría de las cajas. El rango Medios-Graves contiene los armónicos de bajo orden de la mayoría de instrumentos y generalmente se le ve como el rango de presencia de graves.

Por lo tanto necesitamos extraer la información de nuestro sonido para estos rangos seleccionando los elementos correspondientes del resultado de la FFT. Para obtener la frecuencia de cada elemento del resultado de la FFT tendremos que calcular el tamaño de la division de frecuencias (44100/1024 = 43) y multiplicarlo por el índice del array de datos. Teniendo en cuenta esto, la primera componente almacenará el resultado del rango 0-43Hz, la segunda 43-86Hz, la tercera 86-129Hz…

El algoritmo

Asumiendo que k y k+n son los límites del actual rango que estamos procesando y FFT[i] es la amplitud de la frecuencia para la posición i . Podemos definir la energía del rango como:

Tenemos que almacenar este valor junto al de las 42 muestras obtenidas lo largo de 1 segundo para establecer nuestra historia (H).

Ahora la media de la banda puede calcularse utilizando esta historia

Normalmente un valor que excede el valor de la media en más de su mitad es un buen umbral para detectar un pulso. Pero podemos ajustar este factor utilizando la varianza de la historia. En música muy ruidosa, como Hard Rock o Rock N’ Roll, la detección de pulso puede resultar bastante dudosa, por lo que tendremos que bajar el umbral cuando nos encontremos valores altos en su varianza.

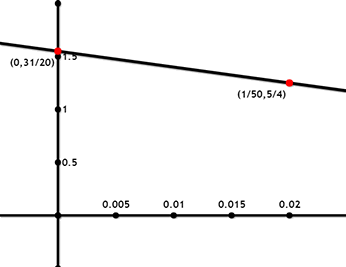
Podemos definir una ecuación lineal (Varianza, Umbral) para representar la relación entre el factor umbral y la varianza. Con (0, 1.55) (0.02, 1.25) como dos de los puntos de esa linea podemos definir su ecuación como:

Los valores del resultado de la FFT se encuentran en rango 0..1 por lo que la varianza estara en rango 0..1 también.

Finalmente un pulso se detecta si:

El código

Ahora ya podemos empezar a modificar la clase C++ SoundManager_Fmod de nuestro tutorial anterior Espectro de Frecuencias utilizando FMOD y UE4 para añadir el algoritmo de detección de beat.

Tendremos que añadir algunas variables, para guardar el buffer de historia, la velocidad de muestreo y el tamaño de ventana, y unas cuantas funciones auxiliares para calcular la media, varianza y el valor umbral. Además de esto vamos a añadir una función para inicializar el detector de pulsos y otra para recuperar el resultado de su análisis, esta ultima se tendrá que llamar despues de la función Update (igual que se hace con getSpectrum_). Para guardar los datos de la Historia vamos a utilizar un contenedor doble cola (deque), con él podemos insertar los nuevos elementos al principio y eliminar los más viejos por el final.

SoundManager_Fmod.h

public:
	...
	void initializeBeatDetector();
	void getBeat(float* spectrum, float* averageSpectrum, bool& isBass, bool& isLowM);
private:
	...
	int _windowSize;
	float _samplingFrequency;

	typedef std::deque<std::vector<float> > FFTHistoryContainer;

	int _FFThistory_MaxSize;
	std::vector<int> _beatDetector_bandLimits;
	FFTHistoryContainer _FFTHistory_beatDetector;

	static void fillAverageSpectrum(float* averageSpectrum, int numBands, const FFTHistoryContainer& fftHistory);
	static void fillVarianceSpectrum(float* varianceSpectrum, int numBands, const FFTHistoryContainer& fftHistory, const float* averageSpectrum);
	static float beatThreshold(float variance);

SoundManager_Fmod.cpp

Para obtener la velocidad de muestreo podemos utilizar la función getFrequency de nuestra instancia canal (FMOD). Tendremos que añadir un par de lineas en la función playSound para recuperar la información de la velocidad de muestreo y calcular el tamaño de la historia para albergar 1 segundo. (_samplingFrequency / _windowSize).

void SoundManager_Fmod::playSound()
{
	_FFTHistory_linear.clear();
	_FFTHistory_log.clear();

	_system->playSound(_sound, 0, false, &_channel);

	_channel->getFrequency(&_samplingFrequency);
	_FFThistory_MaxSize = _samplingFrequency / _windowSize;

	_channel->addDSP(0, _dsp);
	_dsp->setActive(true);
}

InitializeBeatDetector se utilizará para calcular los indices que corresponden a los limites de los rangos que queremos analizar. En este ejemplo estamos utilizando dos rangos, Graves y Medios-graves, solo necesitaremos la información de los elementos del array que estén dentro de su rango de frecuencias.

void SoundManager_Fmod::initializeBeatDetector()
{
	int bandSize = _samplingFrequency / _windowSize;

	_beatDetector_bandLimits.clear();
	_beatDetector_bandLimits.reserve(4); // bass + lowMidRange * 2

	// BASS 60 hz - 130 hz (Kick Drum)
	_beatDetector_bandLimits.push_back( 60 / bandSize);
	_beatDetector_bandLimits.push_back( 130 / bandSize);

	// LOW MIDRANGE 301 hz - 750 hz (Snare Drum)
	_beatDetector_bandLimits.push_back( 301 / bandSize);
	_beatDetector_bandLimits.push_back( 750 / bandSize);

	_FFTHistory_beatDetector.clear();
}

La función getBeat tiene una estructura similar a las funciones getSpectrum_ pero añadiendo el algoritmo de detección de pulso. Calcula la FFT, extrae la información de determinadas frecuencias y aplica el algoritmo para cada rango, devolviendo el resultado de cada uno de los rangos de manera individual. Después de aplicar el algoritmo incrementa el buffer de Historia, eliminando los elementos mas viejos si se supera su limite de capacidad.

void SoundManager_Fmod::getBeat(float* spectrum, float* averageSpectrum, bool& isBass, bool& isLowM)
{
	FMOD_DSP_PARAMETER_FFT* dspFFT = NULL;
	FMOD_RESULT result = _dsp->getParameterData(FMOD_DSP_FFT_SPECTRUMDATA, (void **)&dspFFT, 0, 0, 0);

	if (dspFFT)
	{
		// Only read / display half of the buffer typically for analysis 
		// as the 2nd half is usually the same data reversed due to the nature of the way FFT works.
		int length = dspFFT->length / 2;
		int numChannels = dspFFT->numchannels;

		if (length > 0)
		{
			int numBands = _beatDetector_bandLimits.size() / 2;

			for (int numBand = 0; numBand < numBands; ++numBand)
			{
				int bandBoundIndex = numBand * 2;
				for (int indexFFT = _beatDetector_bandLimits[bandBoundIndex];
					indexFFT < _beatDetector_bandLimits[bandBoundIndex + 1];
					++indexFFT)
				{
					for (int channel = 0; channel < numChannels; ++channel)
					{
						spectrum[numBand] += dspFFT->spectrum[channel][indexFFT];
					}
				}
				spectrum[numBand] /= (_beatDetector_bandLimits[bandBoundIndex + 1] - _beatDetector_bandLimits[bandBoundIndex]) * numChannels;
			}

			if (_FFTHistory_beatDetector.size() > 0)
			{
				fillAverageSpectrum(averageSpectrum, numBands, _FFTHistory_beatDetector);

				std::vector<float> varianceSpectrum;
				varianceSpectrum.resize(numBands);
				fillVarianceSpectrum(varianceSpectrum.data(), numBands, _FFTHistory_beatDetector, averageSpectrum);
				isBass = (spectrum[0] - 0.05) > beatThreshold(varianceSpectrum[0]) * averageSpectrum[0];
				isLowM = (spectrum[1] - 0.005) > beatThreshold(varianceSpectrum[1]) * averageSpectrum[1];
			}
				
			std::vector<float> fftResult;
			fftResult.reserve(numBands);
			for (int index = 0; index < numBands; ++index)
			{
				fftResult.push_back(spectrum[index]);
			}
			
			if (_FFTHistory_beatDetector.size() >= _FFThistory_MaxSize)
			{
				_FFTHistory_beatDetector.pop_front();
			}

			_FFTHistory_beatDetector.push_back(fftResult);
		}
	}
}

Por último se añade el código de las funciones auxiliares que calculan la media, varianza y el factor umbral.

void SoundManager_Fmod::fillAverageSpectrum(float* averageSpectrum, int numBands, const FFTHistoryContainer& fftHistory)
{
	for (FFTHistoryContainer::const_iterator fftResult_it = fftHistory.cbegin();
		fftResult_it != fftHistory.cend();
		++fftResult_it)
	{
		const std::vector<float>& fftResult = *fftResult_it;

		for (int index = 0; index < fftResult.size(); ++index)
		{
			averageSpectrum[index] += fftResult[index];
		}
	}

	for (int index = 0; index < numBands; ++index)
	{
		averageSpectrum[index] /= (fftHistory.size());
	}
}

void SoundManager_Fmod::fillVarianceSpectrum(float* varianceSpectrum, int numBands, const FFTHistoryContainer& fftHistory, const float* averageSpectrum)
{
	for (FFTHistoryContainer::const_iterator fftResult_it = fftHistory.cbegin();
		fftResult_it != fftHistory.cend();
		++fftResult_it)
	{
		const std::vector<float>& fftResult = *fftResult_it;

		for (int index = 0; index < fftResult.size(); ++index)
		{
			varianceSpectrum[index] += (fftResult[index] - averageSpectrum[index]) * (fftResult[index] - averageSpectrum[index]);
		}
	}

	for (int index = 0; index < numBands; ++index)
	{
		varianceSpectrum[index] /= (fftHistory.size());
	}
}

float SoundManager_Fmod::beatThreshold(float variance)
{
	return -15 * variance + 1.55;
}

Conclusión

Este tutorial muestra uno de los métodos utilizados para conseguir una solución rápida y mas o menos precisa para la detección de pulsos. Este método puede utilizarse cuando el rendimiento es mucho más importante que la precisión, como cuando buscamos un análisis en tiempo real. Sin embargo, si quisiéramos una solución más acertada tendríamos que optar por utilizar otro tipo de análisis, como por ejemplo la Transformada Wavelet Discreta (DWT). En el documento Audio Analysis using the Discrete Wavelet Transform de George Tzanetakis, Georg Essl y Perry Cook podemos encontrar una aplicación de la DWT muy bien explicada con el objetivo de definir un algoritmo de detección de pulsos.

En el próximo tutorial vamos a integrar el algoritmo que acabamos de implementar en el visualizador de espectro de frecuencias del tutorial anterior.

Parte 6: Visualizador de pulsos para UE4

Tutorial files

2020/06/22 – Actualizado a Unreal Engine 4.24

Ayudanos con este blog!

El último año he estado dedicando cada vez más tiempo a la creación de tutoriales, en su mayoria sobre desarrollo de videojuegos. Si crees que estos posts te han ayudado de alguna manera o incluso inspirado, por favor considera ayudarnos a mantener este blog con alguna de estas opciones. Gracias por hacerlo posible!