Espectro de frecuencias usando FMOD y UE4

Este es un pequeño tutorial para explicar como extraer un espectro de frecuencias de un sonido para nuestros juegos musicales utilizando UE4 y la librería FMOD. En un tutorial previo ya vimos como configurar el editor de UE4 para incluir la librería FMOD, ahora podemos empezar a hacer algunos experimentos con ella. Para empezar vamos a crear un visualizador para el espectro de frecuencias y un detector de pulsos y ritmo.

Parte 1: Configurando las rutas del proyecto
Parte 2: Usando la librería
Parte 3: Espectro de Frecuencias
Parte 4: Visualizador de espectro para UE4
Parte 5: Algoritmo detector de pulsos
Parte 6: Visualizador de pulso para UE4

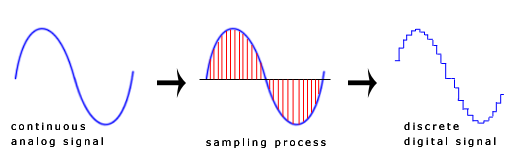
Para poder procesar una onda de sonido con un dispositivo digital la señal continua de la onda debe ser convertida a una secuencia de muestras (señal discreta en el tiempo)

Cuanto mayor sea el número de muestras usadas más se parecerá a la onda original.El teorema de Nyquist dice que para reproducir de manera pracisa una señal, la frecuencia de muestreo debe ser, al menos, el doble de la frecuencia mas alta de la señal. Teniendo en cuenta que el espectro audible esta en el rango 20-20,000 Hz, necesitaremos una frecuencia de muestreo de al menos 40,000 Hz. Esta es una de las razones por las que vemos unos valores de muestreo de 44100 o 48000 en nuestros archivos de audio.
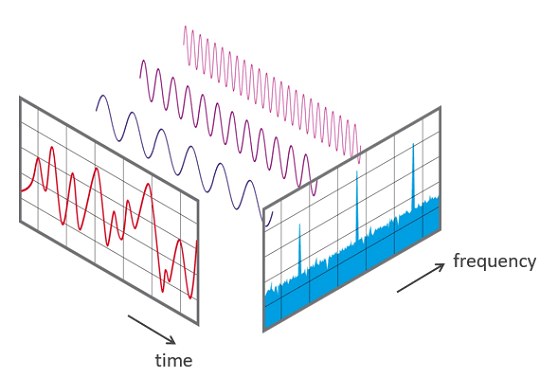
Un espectro de frecuencia es una representación de las frecuencias de un sonido en un instante de tiempo. Cada barra del espectro representa un rango de estas frecuencias.

Todo sonido puede modelado como combinación de ondas sinusoidales con diferentes frecuencias. El espectro muestra la amplitud de la onda para la frecuencia de esa barra.

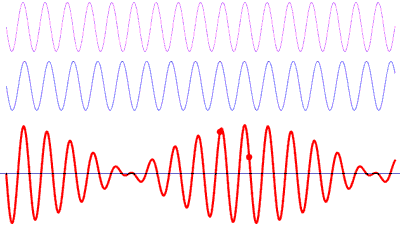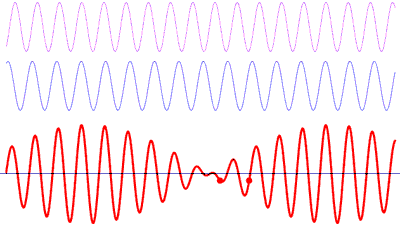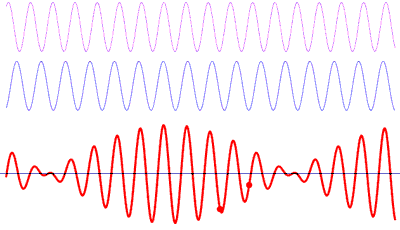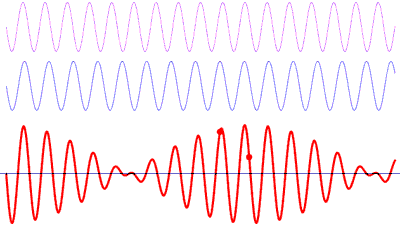
Esto no es diferente a lo que ocurre cuando oímos un sonido. Nuestros oídos toman la suma de todos los sonidos de la habitación en una posición y tiempo concretos.
Para convertir una señal de su dominio de tiempo a su representación en dominio de frecuencias necesitamos utilizar la Transformada Rápida de Fourier

Ahora podemos empezar a modificar la clase C++ de tutoriales anteriores SoundManager_Fmod (Parte 2: Usando la librería). Tenemos dos opciones para procesar nuestro sonido:
El primero de ellos consiste en procesar el sonido completamente,antes de comenzar su reproducción y sincronizar los datos del análisis durante la reproducción. Esto es util si queremos utilizar otras librerías para realizar FFT, como por ejemplo KissFFT. Para extraer la información del sonido de las clases de FMOD tenemos que copiar su información (sin olvidar proteger el acceso durando la copia), y guardarla en un contenedor temporal, podemos utilizar un contenedor para el canal derecho y otro para el izquierdo.

_system->createSound(pathToFile.c_str(), FMOD_LOOP_NORMAL, 0, &_sound);

_sound->getLength(&_length, FMOD_TIMEUNIT_PCM);

//sound lock parameters
void* rawDataPtr;
unsigned int rawDataLength;
void* uselessPtr;
unsigned int uselessLength;

_LRawData.reserve(_length);
_RRawData.reserve(_length);

_sound->lock(0, _length, &rawDataPtr, &uselessPtr, &rawDataLength, &uselessLength);
for (unsigned int t = 0 ; t < _length ; ++t)
{
	_LRawData.push_back(((int*)rawDataPtr)[t]>>16);
	_RRawData.push_back((((int*)rawDataPtr)[t]<<16)>>16);
}
_sound->unlock(rawDataPtr, uselessPtr, rawDataLength, uselessLength);

El problema de esta opción es el tiempo que se necesita, tanto para copiar como para realizar el análisis completo, cuando el archivo de sonido es relativamente grande. Para evitar esto es mejor utilizar un análisis en tiempo real, que es el que finalmente vamos a usar. La primera modificación sera pasar el flag FMOD_CREATESAMPLE en la llamada acreateSound . FMOD_CREATESAMPLE fuerza la descompresión en tiempo de carga, descomprime o decodifica todo el archivo en memoria. Más rápido para la reproducción y más flexible que otros flags.

_system->createSound(memoryPtr, FMOD_OPENMEMORY | FMOD_LOOP_NORMAL | FMOD_CREATESAMPLE, &sndinfo, &_sound);

Para usar el análisis FFT de FMOD tenemos que añadir un procesador de señal digital (DSP) al canal de nuestro sonido. Durante la inicialización de la instancia _system podemos crear y establecer los parámetros de nuestro DSP.

FMOD::DSP*	_dsp;

_system->init(1, FMOD_INIT_NORMAL, NULL);

_system->createDSPByType(FMOD_DSP_TYPE_FFT, &_dsp);
_dsp->setParameterInt(FMOD_DSP_FFT_WINDOWTYPE, FMOD_DSP_FFT_WINDOW_TRIANGLE);
_dsp->setParameterInt(FMOD_DSP_FFT_WINDOWSIZE, _windowSize);

Cuando la variable _channel este inicializada podemos añadirla el DSP anterior al canal y activarlo a continuación.

_system->playSound(_sound, 0, false, &_channel);

_channel->addDSP(0, _dsp);
_dsp->setActive(true);

Para obtener los datos de la FFT tenemos que utilizar la función getParameterData de nuestra instancia DSP con el flag FMOD_DSP_FFT_SPECTRUMDATA. Además de esto, tenemos que llamar a system->update() una vez por tick de juego, o por frame, para actualizar el sistema FMOD. Podemos utilizar el nodo Tick event de UE4 para realizar ambas llamadas.

Espectro Linear

Para realizar un análisis linear del espectro tendremos que dividir los datos en bandas, como nuestro ejemplo tiene un tamaño de ventana de 1024 samples, vamos a agrupar juntas 1024 / num-de-bandas frecuencias en cada banda.

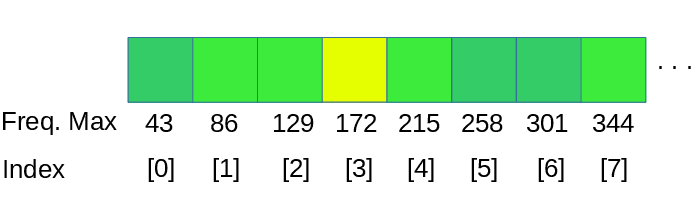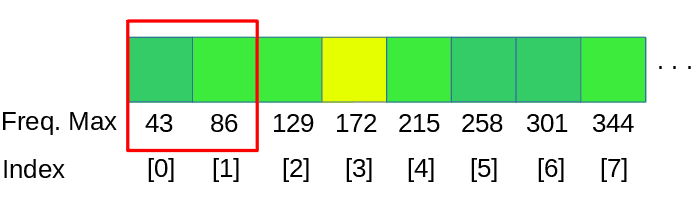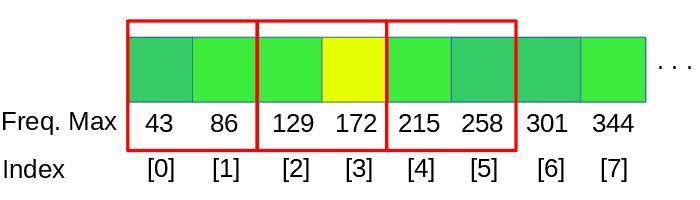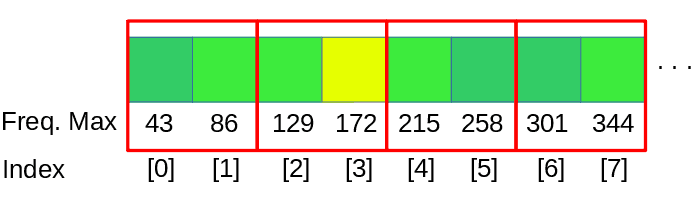
dspFFT->spectrum devuelve la estructura de datos resultante de la FFT por canal y frecuencia, para este ejemplo tenemos que procesar 2 canales, derecho e izquierdo, tomamos la media de los valores de ambos canales.

int SoundManager_Fmod::initializeSpectrum_Linear(int maxBands)
{
	int barSamples = (_windowSize / 2) / maxBands;

	//calculates num fft samples per bar
	_numSamplesPerBar_linear.clear();
	for (int i = 0; i < maxBands; ++i)
	{
		_numSamplesPerBar_linear.push_back(barSamples);
	}
	return _numSamplesPerBar_linear.size(); //effectiveBars
}

void SoundManager_Fmod::getSpectrum_Linear(float* spectrum)
{
	FMOD_DSP_PARAMETER_FFT* dspFFT = NULL;
	FMOD_RESULT result = _dsp->getParameterData(FMOD_DSP_FFT_SPECTRUMDATA, (void **)&dspFFT, 0, 0, 0);
	if (dspFFT)
	{
		// Only read / display half of the buffer typically for analysis 
		// as the 2nd half is usually the same data reversed due to the nature of the way FFT works.
		int length = dspFFT->length / 2;
		int numChannels = dspFFT->numchannels;

		if (length > 0)
		{
			int indexFFT = 0;
			for (int index = 0; index < _numSamplesPerBar_linear.size(); ++index)
			{
				for (int frec = 0; frec < _numSamplesPerBar_linear[index]; ++frec)
				{
					for (int channel = 0; channel < numChannels; ++channel)
					{
						spectrum[index] += dspFFT->spectrum[channel][indexFFT];
					}
					++indexFFT;
				}
				spectrum[index] /= (float)(_numSamplesPerBar_linear[index] * numChannels);
			}
		}
	}
}

initializeSpectrum_Linear calcula cuantas muestras vamos a tomar para cada barra del visualizador de espectro, para una distribución lineal es trivial, vamos a tomar el mismo número de muestras para todas las barras. Esta lógica podria implementarse en la función getSpectrum_Linear directamente, pero queremos mantener una estructura de código similar al siguiente algoritmo de división.
Esto es un espectro linear básico:

El problema que tenemos con este espectro es que agrupamos un montón de información util en las primeras barras perdiendo detalles importantes en las frecuencias más bajas. La mayoría de la información más util se encuentra por debajo de los 15000 Hz.

Espectro Logarítmico

Una mejor manera de agrupar el espectro sería con divisiones logarítmicas de los resultados de la FFT.

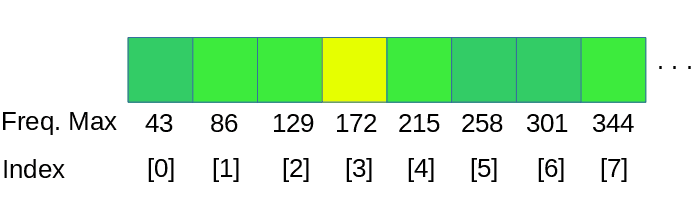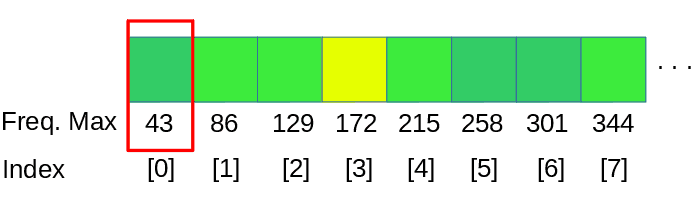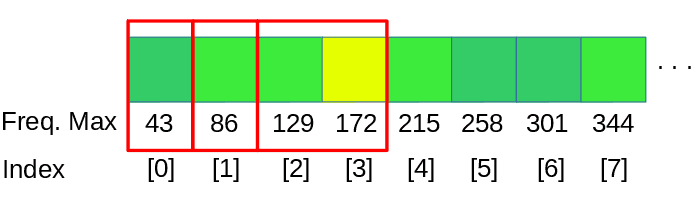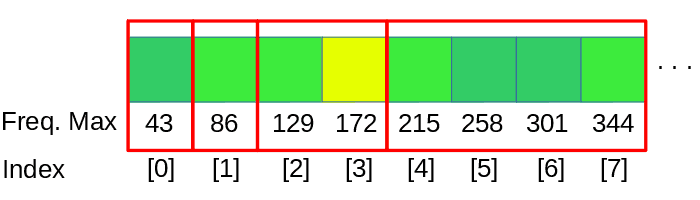
Una manera natural de hacer esto es dividir abarcando octavas. Podemos agrupar las frecuencias con los siguientes rangos (asumiendo un frecuencia de muestreo de 44100 Hz):

0 a 11 Hz
11 a 22 Hz
22 a 43 Hz
43 a 86 Hz
86 a 172 Hz
172 a 344 Hz
344 a 689 Hz
689 a 1378 Hz
1378 a 2756 Hz
2756 a 5512 Hz
5512 a 11025 Hz
11025 a 22050 Hz

Esto nos va a dar 12 bandas, pero ya son más útiles que 32 lineales. Si queremos mas de 12 bandas, podemos dividir cada octava en dos, o tres, el grado de division solo está limitado por el tamaño de ventana de la FFT.
Podemos precalcular estos valores usando el siguiente código:

frequencyOctaves.push_back(0);
for (int i = 1; i < 13; ++i)
{
		frequencyOctaves.push_back((int)((44100 / 2) / (float)pow(2, 12 - i)));
}

Y hacer agrupaciones de los datos de la FFT usando estos límites. Ten en cuenta que las frecuencias por debajo de la primera componente de nuestra FFT no puede representarse en el visualizador., por lo que los rangos 0-11Hz, 11-22Hz y 22-43Hz deben ser agrupados juntos en la primera barra de este ejemplo. La primera componente de la FFT, que corresponde al rango 0-43Hz, se asignará a la primera de las barras, descartando las barras que podrían corresponder a 0-11 y 11-22. Dependiendo de las divisiones de la octava debemos aplicar esta mismo solución a los siguientes intervalos también.
Una vez conocemos cuantas muestras necesita cada una de las barras, ya solo nos queda recorrer los datos de la FFT calculando la media de esas muestras.

int SoundManager_Fmod::initializeSpectrum_Log(int maxBars)
{
	//calculates octave frequency
	std::vector<int> frequencyOctaves;
	frequencyOctaves.push_back(0);
	for (int i = 1; i < 13; ++i)
	{
		frequencyOctaves.push_back((int)((44100 / 2) / (float)pow(2, 12 - i)));
	}

	int bandWidth = (44100 / _windowSize);
	int bandsPerOctave = maxBars / 12; //octaves

	//calculates num fft samples per bar
	_numSamplesPerBar_log.clear();
	for (int octave = 0; octave < 12; ++octave)
	{
		int indexLow = frequencyOctaves[octave] / bandWidth;
		int indexHigh = (frequencyOctaves[octave + 1]) / bandWidth;
		int octavaIndexes = (indexHigh - indexLow);

		if (octavaIndexes > 0)
		{
			if (octavaIndexes <= bandsPerOctave)
			{
				for (int count = 0; count < octavaIndexes; ++count)
				{
					_numSamplesPerBar_log.push_back(1);
				}
			}
			else
			{
				for (int count = 0; count < bandsPerOctave; ++count)
				{
					_numSamplesPerBar_log.push_back(octavaIndexes / bandsPerOctave);
				}
			}
		}
	}

	return _numSamplesPerBar_log.size(); //effectiveBars
}

void SoundManager_Fmod::getSpectrum_Log(float* spectrum)
{
	FMOD_DSP_PARAMETER_FFT* dspFFT = NULL;
	FMOD_RESULT result = _dsp->getParameterData(FMOD_DSP_FFT_SPECTRUMDATA, (void **)&dspFFT, 0, 0, 0);
	if (dspFFT)
	{
		// Only read / display half of the buffer typically for analysis 
		// as the 2nd half is usually the same data reversed due to the nature of the way FFT works.
		int length = dspFFT->length / 2;
		int numChannels = dspFFT->numchannels;

		if (length > 0)
		{
			int indexFFT = 0;
			for (int index = 0; index < _numSamplesPerBar_log.size(); ++index)
			{
				for (int frec = 0; frec < _numSamplesPerBar_log[index]; ++frec)
				{
					for (int channel = 0; channel < numChannels; ++channel)
					{
						spectrum[index] += dspFFT->spectrum[channel][indexFFT];
					}
					++indexFFT;
				}
				spectrum[index] /= (float)(_numSamplesPerBar_log[index] * numChannels);
			}
		}
	}
}

Podemos ver como getSpectrum_Log tiene la misma lógica que getSpectrum_Linear pero utilizando la division logarítmica en vez de la lineal.

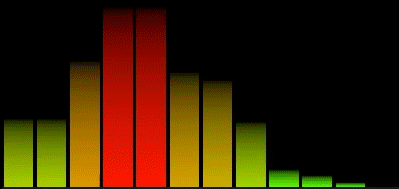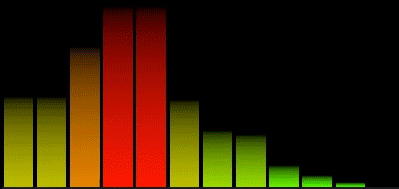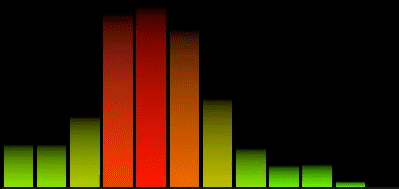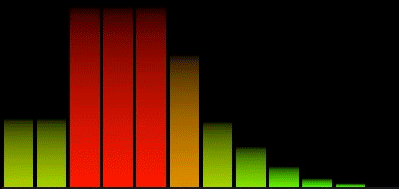
En el siguiente tutorial vamos a diseñar un visualizador para estos valores del espectro utilizando Unreal Engine 4, válido tanto para plataforma Win64 como Android.

Part 4: UE4 spectrum visualizer

Tutorial files

2020/06/22 – Actualizado a Unreal Engine 4.24

Ayudanos con este blog!

El último año he estado dedicando cada vez más tiempo a la creación de tutoriales, en su mayoria sobre desarrollo de videojuegos. Si crees que estos posts te han ayudado de alguna manera o incluso inspirado, por favor considera ayudarnos a mantener este blog con alguna de estas opciones. Gracias por hacerlo posible!